高级语言
程序语言是一个记号系统, 语法 + 语义进行描述
语法
语法:任何语言程序都可以看成是一定字符集(字母表)上的字符串,语法使得这串字符形成一个形式上正确的程序。语法 = 词法规则 + 语法规则
- 词法规则和语法规则定义了程序的形式结构,是判断输入字符串是否构成一个形式上正确的程序的依据
- 单词符号:语言中具有独立意义的最基本结构;一般包括,常数、标识符、基本字、算符、界限符等
- 词法规则:规定了字母表中那些字符串是单词符号;用正规式和有限自动机理论来描述词法结构和进行词法分析
- 语法单位:表达式、子句、语句、函数、过程、程序
- 语法规则:规定了如何从单词符号来形成语法单位;现在多数程序语言使用上下文无关文法来描述语法规则
语义
语义:定义单词符号和语法单位的意义
- 目前,大多数编译程序使用基于属性文法的语法制导翻译方法来分析语义
字母表与符号表
字母表->符号->符号串->句子->语言
字母表:符号的非空有穷集合;例如 $V_1={a, b, c}, V_2={+, -}, \sum = {x| x \in ASCII }$
符号:语言中最基本的不可再分的单位;例如 {a, b, c, +, -, ...}
符号串:字母表中符号组成的有穷序列; 例如 {a, abc, -ab, ...}
空串:不含有任何符号的串
句子:字母表上符合某种规则(词法规则/语法规则)构成的串
语言:字母表上符合某种规则的语句组成;字母表上的语言就是字母表上正闭包的子集
Tips:约定用 $a, b, c, \dots $ 表示符号;用 $\alpha, \beta, \gamma, \dots$ 表示符号串;用$A, B, C, \dots $ 表示符号串的集合
符号串集合的运算
- 连接/乘积运算: 符合语法要求, 需要语义检查
- 自身的连接成为方幂

- 闭包运算:字母表 A 上符号组成的所有串的集合(包括空串)
- 正闭包 $A^+$ 不包括空串的(星)闭包
$$
A^* = A^0 \cup A^1 \cup A^2 \cup \dots \
A^+ = A^1 \cup A^2 \cup A^3 \cup \dots
$$
文法
文法是描述语言的语法结构的形式规则

非终结符:V_N, 出现在规则的左部、用 <> 括起来、表示一定语法概念的词
终结符:V_T, 语言中不可再分割的字符串(包括单个字符组成的串),是组成句子的基本单位
开始符号:又称为识别符号,表示所定义的语法范畴的非终结符
产生式:用来定义符号串之间关系的一组(语法)规则
推导:从开始符号开始,通过使用产生式的右部取代左部,最终能产生语言的一个句子的过程
规约:推导的逆过程,从给定的源语言的句子开始,通过规则的左部取代右部,最终达到开始符号的过程

句型:从文法的开始符号 S 开始,每步推导(包括 0 步推导)所得到的字符串
句子:仅含终结符的句型
语言:由 S 开始通过 1 步或 1 步以上推导所得的句子的集合
扩充的 BNF 表示
- 小括号提取因子:
U -> ax|ay|az—>U -> a(x|y|z) - 中括号表示任选符号:
<Int>->[+|-]<number>{<number} - 大括号重复次数指定:
<Identifier>-><alpha>{<alpha>|<number>}^5_0
文法与语言的形式定义
Chomsky 将文法 G 定义为四元组 $G=(V_N,V_T,P,S)$, (非终结符号集合, 终结符号集合, 产生式的有穷集合, 文法开始符号)

0 型文法: 短语文法或无限制文法; 限制产生式左侧至少有一个非终结符; 图灵机, TM, 即可识别 0 型语言
- 任何的 0 型文法都是递归可枚举的
1 型文法:长度增加文法, 因为是累积递增的, 所以又称上下文有关文法(CSG, Context-Sensitive Grammar); 线性界限自动机, LBA, 用于识别 1 型语言
- 开始符号若产生空集那开始符号必须在左侧
- 其余的推导必须是递增式推导, 即 $\alpha \rightarrow \beta$ 必须有 $|\beta| > |\alpha|$

2 型文法: 上下文无关文法(CFG, Context-Free Grammer, 非终结符的替换不必考虑上下文); 下推自动机, PDA, 可用于识别 2 型语言
- 产生式左侧一定是非终结符

3 型文法:正规文法、右线性文法或左线性文法;有限状态自动机即可识别 3 型语言
- 产生式左侧一定为非终结符
- 产生式右侧一定有终结符
- 产生式右侧可以有非终结符,如果非终结符均在左,则称左线性文法;反之右线性文法


词法分析与语法分析中的限制:
- 不存在 P -> P 的限制
- 产生式中出现的任何非终结符 P 必须有用(P 必须能推到终结符)
文法的简化
在文法中,有些产生式对推导不起作用,要删除掉
- 某个产生式在推导过程中永远不会被用到,即由开始符号推导,永远推不到的左部的非终结符
- 如永远导不出终结符串的产生式
- 如形如 P→P 的产生式
简化步骤:
- 查找有无形如 P→P 的产生式,若有则删除
- 若某个产生式在推导过程中永远不会被用到,删除它
- 若某个产生式在推导过程中不能从中导出终结符,删除它
- 最后,整理所有剩余产生式,就得到简化的文法
无空串产生式的 CFG
满足条件:
- P 中要么不含空串产生式,要么只有 S→空串
- 若 S→空串,则 S 不出现在任何产生式右部
构造算法:
- 由文法 G 找出所有经过若干步推导能推出 空串 的非终结符, 放在 V0 集合中
- 按照下列步骤构造 G’ 的产生式集合 P’
- 若 V0 集合中的某元素出现在某产生式的右端,则将它变成两个产生式:分别以 空串 和其原型带入, 加入 P’
- 其他产生式出去 空串 产生式后也加入 P’
- 如果 P 中有产生式 S -> 空串,将它在 P’ 中改为 S’ -> 空串 | S 的形式

语法树
用来表示语言句子结构的树, 使用语法树可以使语法分析过程直观、形象,易于判断文法二义性
子树:除叶子结点之外的任意结点连同它的所有子孙结点构成子树(包括这个树本身)
修剪子树:剪去子树树根的所有孩子节点
句型:在一棵语法树生长过程中的任何时刻,所有那些叶子结点排列起来就是一个句型
短语:子树的末端符自左至右连成的串(可以包含非终结符),相对于子树树根而言称之为短语
- 简单短语:一步推导得到的短语
- 句型的短语:该句型中哪些符号串可构成某子树根的短语(所有孩子节点)
句柄:句型中最左简单短语;句柄是最左归约时要寻找的简单短语
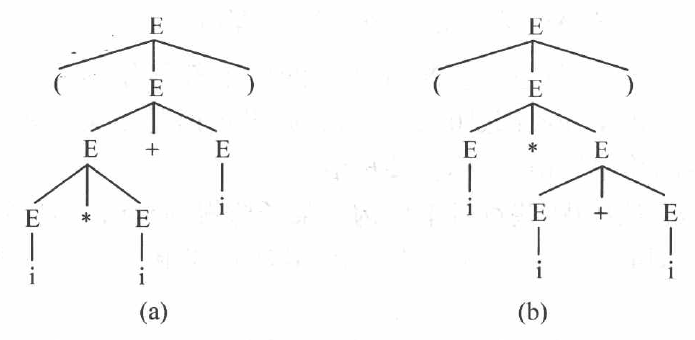
文法二义性
句子二义性:如果文法的一个句子存在对应的两棵或两棵以上的语法树,则该句子是二义的